Luận bàn về Complexity - Big O notation

Đây là thứ bắt buộc phải thạo nếu muốn tối ưu thuật toán tốt hơn và ko bị nhà tuyển dụng đấm sml -_-

Với mỗi thuật toán, ta cần có 1 thang đo thuật toán đó nhanh hay chậm, phức tạp hay đơn giản, tối ưu hay thừa thãi... Và từ đó người ta đã định nghĩa ra thuật ngữ the complexity of an algorithm. Complexity có 2 loại:

• Time complexity

• Space complexity

Trước khi đi sâu hơn vào 2 loại trên, ta cần phải hiểu 1 chút về thang đo chung cho complexity là gì, ta sẽ lấy thang đo theo time complexity cho quen thuộc hơn:

Big O notation

Ta đã quen vs các thang đo độ dài như cm, m, km... hay khối lượng như g, kg, t..., vậy ở trong thuật toán ta sẽ có Big O.

Nói nôm na thì Big O diễn tả số bước nhiều nhất mà 1 thuật toán có thể phải chạy trong 1 chương trình. Sở dĩ phải nhấn mạnh nhiều nhất và có thể vì các input, process của mỗi thuật toán sẽ không cố định, với mỗi input khác nhau sẽ cho ra số bước để chạy khác nhau (vì side cases).

Vậy nên ta cần scale cái sự biến thiên này về 3 mức cơ bản ít nhất (best case), nhiều nhất (worst case) và trung bình (average or expected case). Big O sẽ ký hiệu cho upper bound, trong nhiều nghĩa sẽ giống như worst case, 2 loại còn lại ta sẽ đề cập tới chúng sau.

Ví dụ: Tìm 1 phần tử trong 1 array có n phần tử bằng linear search, trường hợp tệ nhất là ta sẽ phải chạy hết các phần tử, thế nên thuật toán sẽ chạy hết n bước. Như vậy ta có O(n).

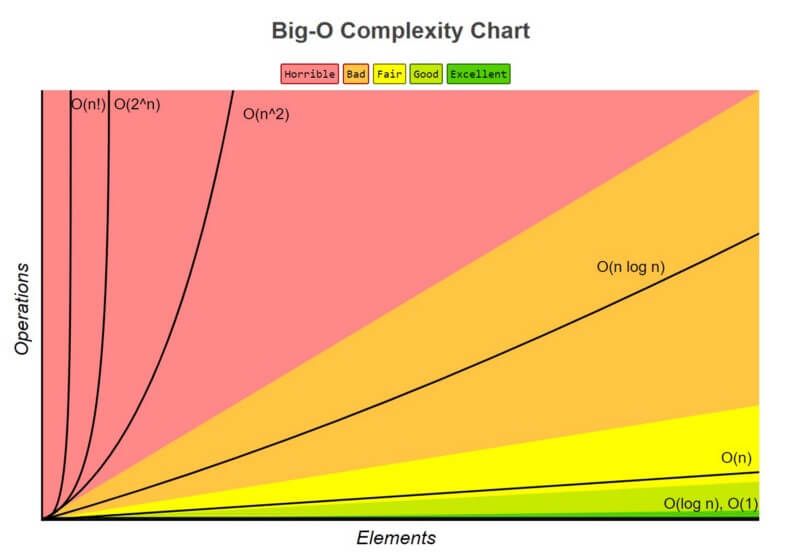
Để có thể dễ scale hơn, ta cũng có 1 số typical Big Os từ nhanh tới chậm như sau (phổ biến trong đa số các thuật toán hiện nay):

• O(1): constant (best)

• O(logn): logarithmic (ngon)

• O(n): linear (nah)

• O(nlogn): logarithmic (but worse than logn) (nah)

• O(n^k): polynomial (tệ) - phổ biển nhất 2 loại quadratic: O(n^2) và cubic: O(n^3)

• O(2^n): exponential (tệ)

• O(n!): factorial (tệ)

Big Theta and Big Omega

Như đã kể trên, ngoài Big O (worst case) ra, ta còn có 2 loại nữa, gọi là Big Theta và Big Omega:

• Big omega: Ký hiệu là Ω(). Tượng trưng cho lower bound, hiểu đơn giản nhất là sẽ giống như best

case.

After all, you know that it won't be faster than thoses runtimes (Gayle Laakmann McDowell - Cracking the Coding Interview)

• Big Theta: Ký hiệu là Θ(). Là cả O và Ω, hiểu theo kiểu giữa O và Ω cũng ko sai.

2 ký hiệu trên sẽ được sử dụng nhiều trong học thuật. Còn trong thực tiễn, thì nhà nhà dùng O cho nó có sự thống nhất hơn.

Định nghĩa thì đơn giản thế thôi, nhưng vấn đề là làm sao để ta có thể ước lượng (đếm) số bước 1 cách chính xác nhất?

Câu trả lời đầu tiên: Vẫn cứ là luyện nhiều thoy :v

Câu trả lời tiếp theo: thông qua luyện nhiều như trên, ta nhận ra sẽ có nhiều mẫu code chung mà ta có thể đưa về các typical Big O như đã liệt kê, chẳng hạn:

Check các vòng lặp for, while

Ta biết rằng mỗi vòng lặp với n phần tử sẽ tốn O(n) time.

logn runtimes

Ta sẽ thấy O(logn) trong các trường hợp+ Trong các chuỗi n phần tử, ở mỗi vòng lặp, ta chia nhỏ số phần tử cần xử lý ra. Ví dụ:

""" We divide n by 2 for each iteration """

n = 16
n = 8     """divided by 2"""
n = 4     """divided by 2"""
n = 2     """divided by 2"""
n = 1     """divided by 2"""

""" The program runs 4 times, which is equivalent to log base 2 of 16 """

Recursive runtimes

Với đệ qui thì nó khá là lừa. Chẳng hạn với quả code này

int f(int n) {
  if (n <= 1) {
    return 1;
  }
  return f(n-1) + f(n-1);
}

Nhiều người sẽ tưởng là O(n^2) vì nhìn qua nghĩ là mỗi phần tử n sẽ chạy 2 lần, nhưng nope, ko dễ thế dou fren :))) Thử break out quả code trên ra với n = 4 đi:

Iter 0: f(4)                                    => 1 f()
Iter 1: f(3) f(3)                               => 2 f()
Iter 2: f(2) f(2) f(2) f(2)                     => 4 f()
Iter 3: f(1) f(1) f(1) f(1) f(1) f(1) f(1) f(1) => 8 f()

Như vậy ta thấy cái thuật toán trên sẽ call tới f() tổng cộng 1 + 2 + 4 + 8. Suy ra nó sẽ chạy 2^0 + 2^1 + 2^2 + 2^3 lần. Vì sao lại là 2?

Dễ thấy ở đoạn code trên, mỗi khi ta gọi tới 1 f(), thì hóa ra nó lại gọi tới 2 lần f() nhỏ hơn, như vậy mỗi level sẽ phải nhân 2 thoy.

Cuối cùng thì kết quả sẽ là O(2^n).

Thông qua ví dụ trên, ta có thể đúc rút ra được là đệ qui chạy theo exponential time và một mẹo tìm big O riêng cho đê qui: Với 1 function đệ qui, ta xem xem nó sẽ gọi tới bao nhiêu function nhỏ. Gọi tới 1 function thì sẽ là O(1^n), 2 function sẽ là O(2^n), 3 funtion sẽ là O(3^n), ... , k functions => O(k^n)

Rút gọn Big O

Như ví dụ ở trên, khi tính tất cả các phần hợp lại, ta sẽ được kết quả cuối cùng là O(2^0 + ... + 2^n). Nhưng dễ thấy cái kết quả này nhìn nó sợ vcđ =))), cho nên là ta cần rút gọn lại nhìn cho ổn chứ ko thì chầm cảm cmn mất.

Vậy rút gọn thế nào?

Ta sẽ tìm phần nào lớn nhất và đại diện tiêu biểu nhất trong thuật toán (the most dominant). Như ở ví dụ trên thì ta thấy lớn nhất là 2^n. cuối cùng kết quả là O(2^n) ~

Time complexity

Chính là mấy cái nãy giờ ta nói tới, ước lượng số bước chạy của thuật toán.

Tối ưu time complexity chính là làm sao để giảm big O, ví dụ giảm O(n^2) xuống O(n), etc...

Cái việc tối ưu này cực kỳ quan trọng. Thử tưởng tượng, nếu có mỗi bước chạy trong ~3ms và n = 1 triệu, với mỗi độ phức tạp, ta sẽ có thời gian tương đương như sau:

O(1)    =>    ~3ms
O(n)    =>    50 phút
O(n^2)    =>    250 phút
O(2^n)    =>    7.8*10^11 ngày

💀💀💀

Space complexity

Đây là để tính dung lượng mà 1 thuật toán chiếm ngoại trừ input của nó.

Với cách để tính space complexity thì ta chỉ cần tìm xem trong thuật toán phải có phải tạo thêm dữ liệu nào không.

Thang đo cũng tương tự với time complexity, ví dụ:+ Xuất phát từ O(1) tượng trưng cho 1 var element => Với n elements như array, string, etc.., ta sẽ được O(n).