Dynamic Programming: 0-1 Knapsack

Đây là phần 2 trong bộ 5 notes về Dynamic Programming của tôi

1 cái knapsack trong t.anh đc dịch ra là 1 cái balo mà mấy ông leo núi hoặc đi lính hay mang, để chứa đồ ăn, quần áo, dụng cụ etc... Cái Knapsack problem, như tên gọi, là vấn đề mà yêu cầu ta tìm ra được kết quả tối ưu nhất từ 1 lượng items nhất định sao cho chúng ko vượt quá một giới hạn cho trước (hay còn gọi là sức chứa - capacity).

Ở câu hỏi điển hình của 0/1 knapsack, ta được cho trước N loại items, mỗi item có 1 trọng lượng weight cùng 1 giá trị value, và ta có 1 cái balo (knapsack) có sức chứa tối đa là capacity. Yêu cầu đề bài là giá trị lớn nhất mà balo có thể chứa các items là bao nhiêu, biết rằng số lượng lớn nhất mà 1 loại item được cho vào balo là 1?

Example

Đi vào ví dụ cụ thể, ta có:

item 1: [$1, 1kg]
item 2: [$2, 1kg]
item 3: [$2, 2kg]
item 4: [$10, 4kg]
item 5: [$4, 12kg]
int N = 5;
int Capacity = 15;
vector<int> values { 1, 2, 2, 10, 4 };
vector<int> weights { 1, 1, 2, 4, 12 };

Mỗi item chỉ có số lượng là 1.

Output sẽ là các items 1,2,3,4 với giá trị 1 + 2 + 2 + 10 = $15

Vậy chương trình sẽ chạy như thế nào để ra được kết quả trên?

Solution

Dưới đây tôi sẽ diễn giải lại đáp án theo thứ tự nhé: brute force -> memoization -> tabular

Brute force

Bắt đầu với vét cạn. Bổ cái suy nghĩ của ta ra nào. Dễ thấy ở đề bài ta đc yêu cầu là tìm giá trị tổng lớn nhất mà cái balo có thể chứa. Nói cách khác ta cần tìm đc 1 tập hợp các items sao cho tổng giá trị của chúng là lớn nhất, với điều kiện tổng trọng lượng ko đc vượt quá sức chứa tối đa của balo. Vậy ta có thể suy ra bài này là 1 bài toán tìm tập hợp (combination).

Để có đc tập hợp có giá trị lớn nhất, ko còn cách nào khác ngoài việc ta phải biết được giá trị của toàn bộ các tập hợp khác nhau mà các item có thể tạo ra theo yêu cầu đề bài. Well, ko biết kết quả thì sao mà ta so sánh đc 🙂

Chính vì thế, chương trình của ta sẽ phải tìm toàn bộ các tập hợp này, check tổng giá trị của chúng để rồi cập nhật giá trị lớn nhất. Ở 1 bài toán tìm tập hợp, cách để ta có thể check hết các trường hợp chính là sử dụng đệ quy, và để giải quyết bài này, ta áp dụng đệ quy theo ý tưởng như sau:

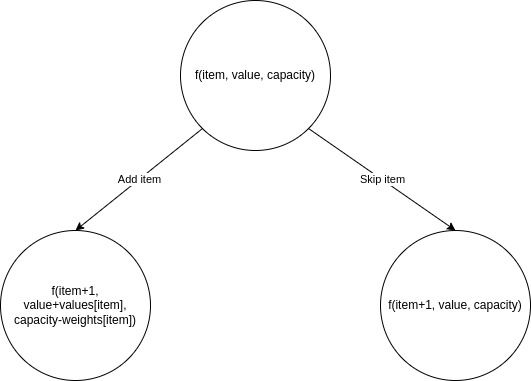
0-1 knapsack brute force approach

Đệ quy đi hết các items, ở mỗi item, ta có 2 lựa chọn xử lý chúng:

Cuối cùng với ý tưởng trên, ta hình thành 1 graph dạng tree

int knapsack01(int itemIndex, int capacity) {
  // Base case
  if (itemIndex >= N || capacity <= 0) return 0;

  int skipItemValues = knapsack01(itemIndex + 1, capacity);
  int addItemValues = (capacity - weights[itemIndex] >= 0) ?
    knapsack01(itemIndex + 1, capacity - weights[itemIndex]) + values[itemIndex] : 0;

  return max(addItemValues, skipItemValues);
}

// Call the function when starting the program
knapsack01(0, Capacity);

Ở cách vét cạn này, ta chạy hết đc chương trình với độ phức tạp là O(2^N) vì phải gọi tới 2 hàm đệ quy và stack đệ quy có thể khiến ta tốn tới O(N) bộ nhớ

Memoization

Debug quả vét cạn trên phát, bắt đầu từ f(0,15) tượng trưng cho knapsack01(0,Capacity) đi:

start             => f(0,15)
value=1 weight=1  => f(1,15)  ...
value=2 weight=2  => f(2,15)  ...
value=2 weight=2  => f(3,15)  f(3,13)  ...
value=10 weight=4 => f(4,15)  f(4,9)   f(4,13)  f(4,11)  ...
value=4 weight=12 => f(5,15)  f(5,3)   f(5,9)   f(5,-3)  f(5,13)  f(5,11)  f(5,11)

Xì tốp, ta thấy được rằng f(5,11) đã lặp lại 2 lần. Điều này có nghĩa là ta hoàn toàn có thể dùng DP để lưu f(5,11) lại, từ đó tiết kiệm đc thời gian gọi đệ quy. Ta có thể lập bảng memoization dựa trên 2 biến đang biến thiên liên tục là itemIndex và capacity. Suy ra:

vector<vector<int>> dp (N, vector<int> (Capacity+1));
int knapsack01(int itemIndex, int capacity) {
  // Base case
  if (itemIndex >= N || capacity <= 0) return 0;

  if (dp[itemIndex][capacity] != 0) return dp[itemIndex][capacity];

  int skipItemValues = knapsack01(itemIndex + 1, capacity);
  int addItemValues = (capacity - weights[itemIndex] >= 0) ?
      knapsack01(itemIndex + 1, capacity - weights[itemIndex]) + values[itemIndex] : 0;

  dp[itemIndex][capacity] = max(addItemValues, skipItemValues);
  return dp[itemIndex][capacity];
}

Tabular

Làm đc memoization rồi, giờ thử nghĩ ngược lại theo hướng bottom-up lên xem. Vì các tập hợp phụ thuộc vào giới hạn capacity, nên ta có thể build up capacity dần dần từ 0...Capacity để tìm ra được tập hợp có giá trị lớn nhất. Để làm đc kiểu bottom-up này, ta sẽ lập nên 1 bảng với các dòng là các item và các cột là các mức cacacity.

Ở mỗi level capacity, ta cũng lại có 2 lựa chọn: add item hoặc skip item, ta thử 2 lựa chọn đấy rồi lưu giá trị lớn nhất vào 1 ô [item, capacity].

Vậy là ta có đoạn code như sau:

vector<vector<int>> dp (N, vector<int> (Capacity+1));
int knapsack01() {
  // We skip the capacity 0
  for (int i = 0; i < N; i++) {
    for (int j = 1; j < dp[0].size(); j++) {
      // At item 0, the bag can only contain the item with the capacity larger than its weight
      if (i == 0) {
        if (weights[i] <= j) dp[i][j] = values[i];
      } else {
        // Skip item
        dp[i][j] = dp[i-1][j]
        // Add item
        if (j - weights[i] >= 0) {
          dp[i][j] = max(dp[i][j], dp[i-1][j-weights[i]] + values[i]);
        }
      }
    }
  }
  return dp[N-1][Capacity];
}

Cả 2 cách Memoization và Tabular đều giúp ta tối ưu đc độ phức tạp từ O(2^N) xuống còn O(N*Capacity) time và O(N*Capacity) bộ nhớ

Follow up

1 cách để nhận biết dạng 0/1 Knapsack này chính là ta để ý xem liệu ta có cần tìm combination trong 1 giới hạn nào đó ko, cùng với số lượng tối đa có phải là 1 hay ko. Nếu có thì triển thoy :v

Sample questions