June 27, 2023

Dynamic Programming: Palindromic Subsequence

Đây là phần 5 trong bộ 5 notes về Dynamic Programming của tôi

Sơ qua về palindrome: aabaa aabbaa

1 palindromic sequence ám chỉ 1 chuỗi con palindrome trong 1 chuỗi chính. Trong 1 chuỗi ta có thể tạo thành khá nhiều chuỗi con palindrome khác nhau với độ dài khác nhau.

Ta đã biết để xử lý 1 palindromic string thì khá đơn giản, nhưng xử lý các chuỗi con palindrome thì ngược lại. Nó sẽ gần như tương tự với việc ta phải xử lý tập hợp các chữ cái sao cho chúng hình thành đc 1 chuỗi dạng palindrome, và với việc giải quyết các tập hợp, ta lại có thể nghĩ ngay đến DP.

Example

Lấy ví dụ điển hình của dạng bài DP liên quan tới palindrome nhé

Cho 1 string BBABCBCAB, tìm chuỗi con palindrome có độ dài lớn nhất trong string đó

string s = "BBABCBCAB";

Ta có thể xác định đc nhiều chuỗi con palindrome trong chuỗi s trên như BAB, BB, BCB, BCBCB, BABAB, ABCBA, BABCBAB, etc... Và trong tất cả chuỗi con đấy, ta lấy ra được chuỗi BABCBAB có độ dài lớn nhất, như vậy ta trả về kết quả là BABCBAB

Vậy chương trình của ta sẽ chạy ntn để có đc kết quả trên?

Solution

Brute force

Vét cạn nhất? Rõ ràng là ta phải thử mọi tập hợp có thể tạo thành 1 chuỗi con palindrome để check xem con nào lớn nhất rồi. Cái khó ở đây là làm sao để ta check đc toàn bộ chuỗi con ấy?

Ôn lại 1 chút ở dạng bài xử lý 1 chuỗi palindrome, ta sẽ cần 2 pointers: 1 cái bắt đầu ở đầu chuỗi (left), 1 cái bắt đầu ở cuối chuỗi (right), rồi tiến lại gần nhau. Ở đây ta cũng áp dụng phương thức tương tự như thế.

Để ý rằng, với 2 pointers đầu cuối đó, nếu chúng chỉ tới 2 chữ cái giống nhau, ta có thể hình thành 1 chuỗi con palindrome; và vì đề bài yêu cầu tìm chuỗi lớn nhất, ko lý nào ta lại bỏ qua chúng. Vậy là ta có trường hợp đầu tiên

if (s[left] == s[right]) f(left, right) = f(left+1, right-1) + 2

Ta sẽ cộng 2 để biểu diễn cho việc cộng dồn 2 chữ cái giống nhau vào chuỗi palindrome của ta

Giờ, nếu 2 chữ cái khác nhau thì sao?

Ta sẽ có 2 options cho pointers của ta để có thể duyệt toàn bộ tập hợp chữ cái của chuỗi chính:

Di chuyển left sang phải 1 index, giữ nguyên right => f(left+1, right)
Di chuyển right sang trái 1 index, giữ nguyên left => f(left, right-1)

Vì là 2 chữ cái khác nhau, ta ko thể đưa vào chuỗi palindrome của ta đc, vậy nên sẽ ko cộng gì cho 2 option này cả, thay vào đó ta sẽ lấy giá trị lớn nhất của chúng => max( f(left+1, right), f(left, right-1)).

int lps(string& s, int left, int right) {
  ^{// Base case}
  if (left == right) return 1;
  if (left > right) return 0;

  ^{// Call to recursive functions}
  if (s[left] == s[right]) return lps(s, left+1, right-1) + 2;
  else return max(lps(s, left+1, right), lps(s, left, right-1));
}

lps(s, 0, s.size()-1);

Cách này ta có thể gọi đến nhiều nhất 2 hàm đệ quy mỗi stack, vậy là có thể tốn tới O(2^n) time với n là độ dài của chuỗi s. Còn bộ nhớ thì nó có thể tiêu tốn tới O(n) với số stack tối đa bằng với độ dài chuỗi s.

Memoization

Ở cách trên, rõ ràng 2 pointers sẽ bị lặp lại index giống nhau nhiều lần, vì thế ta có thể sử dụng 1 bảng DP để lưu lại giá trị lớn nhất của mỗi index của 2 pointers. Ta sẽ sử dụng mảng 2 chiều với mỗi chiều có n phần tử tương ứng với từng index left, right của s.

vector<vector<int>> dp (n, vector<int>(n));
int lps(string& s, int left, int right) {
  ^{// Base case}
  if (left == right) return 1;
  if (left > right) return 0;
  if (dp[left][right] != 0) return dp[left][right];

  ^{// Call to recursive functions}
  if (s[left] == s[right]) dp[left][right] = lps(s, left+1, right-1) + 2;
  else dp[left][right] = max(lps(s, left+1, right), lps(s, left, right-1));

  return dp[left][right];
}

Cách tối ưu này giúp ta giảm thời gian chạy xuống còn có O(n^2) với O(n^2) bộ nhớ cho bảng dp

Tabular

Giờ lại bắt đầu từ bottom-up. Ở 2 cách trên, ta đều tiếp cận input bằng cách chia nhỏ toàn bộ chuỗi. Cách này thì ngược lại, ta xây dựng dần dần từ từng chữ cái 1 của chuỗi đó, vì 1 chữ cái cũng đc tính là 1 chuỗi con palindrome rồi.

Ta sẽ tiến hành duyệt 1 bảng dp nxn cho cách này, index cho hàng dọc (i) tương ứng với left, index cho hàng ngang (j) tương ứng với right.

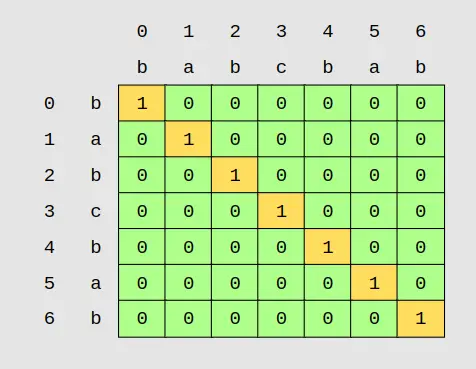
Ta nhận thấy tại i == j, 1 chữ cái trong input string đc biểu diễn => Ta sẽ gán 1 vào dp[i][j] với mọi i == j.

Vì i == j biểu diễn 1 và chỉ 1 chữ cái trong chuỗi, ta sẽ dừng duyệt bảng nếu index vượt qua i hoặc j, hay nói cách khác, ta sẽ chỉ cần phải duyệt 1 nửa bảng dp tương ứng với 1 tam giác, còn đg chéo i == j trong bảng đóng vai trò là đường biên giới cho tam giác.

Ở mỗi cell với i != j, ta cần check xem s[i] có bằng s[j] ko?

Nếu có, ta có thể cộng dồn 2 chữ cái vào chuỗi con palindrome => dp[i][j] = dp[i+1][j-1] + 2
Nếu ko, ta lấy kết quả max từ 2 trường hợp left+1 và right-1 => dp[i][j] = max(dp[i+1][j], dp[i][j-1]).

Vì ta cần lấy kết quả từ [i+1] (ô dưới ô hiện tại) và (ô trái ô hiện tại), ta sẽ phải bắt đầu duyệt bảng từ tọa độ n-2 đi lên trên (ô xanh dưới cùng của tam giác bên phải) vả trả về giá trị cuối cùng ở ô bên phải trên cùng

Tabular visualization — Tabular solution visualization (Credit: educative.io)

vector<vector<int>> dp (n, vector<int>(n));
int lps(string& s) {
  for (int c = 0; c < n; c++) dp[c][c] = 1;
  for (int i = n-2; i >= 0; i--) {
    for (int j = i+1; j < n ; j++) {
      if (s[i] == s[j]) dp[i][j] = dp[i+1][j-1] + 2;
      else dp[i][j] = max(dp[i+1][j], dp[i][j-1]);
    }
  }
  return dp[0][n-1];
}

Cách này sẽ chỉ tốn của ta O(1/2*n^2) => O(n^2) time với bộ nhớ là O(n^2) cho bảng dp.