Luận bàn về Subsets

Đến phần ta cần sử dụng nhiều đệ quy rồi đây @@. Ở post này ta sẽ nói tới pattern Subsets, đây là pattern giúp ta giải quyết các bài toán yêu cầu tìm permutations và combinations ko lặp của các elements trong 1 data structure.

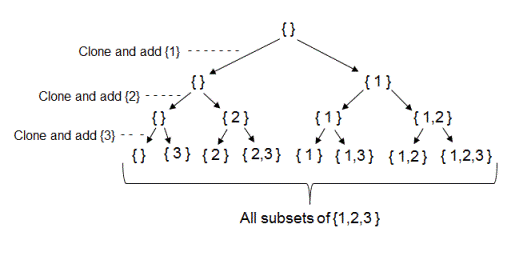
Ví dụ, 1 array [1,2,3]. Ta có các subsets như sau

{1}, {2}, {3}, {1,2}, {1,3}, {2,3}, {1,2,3}

Ý tưởng là ta sẽ xây dựng nên các subsets từ từng elements trong array. Cụ thể trong ví dụ trên:

  1. Ta bắt đầu với 1 tập rỗng {}. Từ tập rỗng này ta generate ra 2 array mới từ 2 option: bỏ qua element 1 và thêm element 1 vào trong array. Như vậy ta đc:

    {}, {1}

  2. Ta lưu tập hợp 2 array trên, rồi với mỗi array ta kết hợp với element 2 bằng 2 cách như ở bước 1. Ta có;

    {}, {2}, {1}, {1,2}

  3. Áp dụng tương tự với tập hợp các array có đc ở bước 2. Ta sẽ đc:

    {}, {3}, {2}, {2,3}, {1}, {1,3}, {1,2}, {1,2,3}

Như vậy bỏ qua tập rỗng ở đầu đi thì ta có được kết quả rồi.

Subset example illustration

Áp dụng vào đệ quy, ta sẽ có pseudocode như sau;

function(saveArrays, inputIndex):

  If inputIndex >= inputArray.size:
    Return saveArrays
  Initialize size = saveArrays.size

  Repeat
  For i from 0 to size-1:
    Initialize newArray = saveArrays[i]
    Append inputArray[inputIndex] to newArray
    Append newArray to saveArrays
  End repeat

  Return function(saveArrays, inputindex+1)

Snippet

vector<vector<int>> subsets(vector<vector<int>>& saveArrays, int inputIndex) {
  if (inputIndex >= inputArray.size()) {
    return saveArrays;
  }

  int size = saveArrays.size();

  // Add new arrays with the new element to the newArrays
  for (int i = 0; i < size; i++) {
    vector<int> newArray (saveArrays[i]);
    newArray.push_back(inputArray[inputIndex]);
    saveArrays.push_back(newArray);
  }

  return subsets(saveArrays, inputIndex+1);
}

Follow up

Sample questions