Luận bàn về Union Find (Disjoint Set)

Trong các bài toán với graph của coding interviews, ngoài việc sử dụng BFS với DFS ra, thì còn có 1 phương thức khác khá nổi tiếng đc gọi là Union Find. Đây là phương thức chuyên trị các yêu cầu xác định sự kết nỗi giữa 2 node, mở rộng ra là 1 nhóm các node kết nối với nhau trong đồ thị. Phương pháp này sẽ cho ta 1 cách tiếp cận khá mới mẻ trong việc xử lý graph nên với những ai chưa quen thuộc về graph sẽ cảm thấy đây là 1 dạng rất khó. Thú thực đây là dạng đầu tiên tôi đc học khi bắt đầu môn algo & data structures và lần đó tôi chẳng hiểu mô tê cái mọe gì @@

Vì đây là pattern khá phức tạp nên ta cần overview qua từng phần nhỏ nhé

Initialization

Đầu tiên, ta cần phải nắm rõ đc cách Union Find (UF) sắp xếp các node vào trong 1 cấu trúc dữ liệu riêng của nó. Để có thể truy cập từng node một, UF sẽ phải đặt riêng cho mỗi node 1 id độc nhất, và 1 reference tới node nó kết nối. Cách đơn giản nhất để làm đc điều này đó là sử dụng array, với index tượng trưng như id của node, và giá trị trong index đó ta quy định là id của node ta kết nối tới (tưởng tượng giống như index hiện tại trỏ tới array[index] của nó)

Ở điểm bắt đầu, tất cả ids trong array đều sẽ là root node, sau đó thông qua các method của UF ta sẽ dựa vào input để xây dụng kết nối giữa các node với nhau.

Root node ở đây ta quy ước là index của array mà tại đó array[index] = index (1 node kết nối với chỉ chính nó). Sở dĩ ta lại gọi là root node là vì qua các bước kết nối các node lại với nhau bằng UF, ta sẽ có được 1 đồ thị dạng tree biểu diễn sự kết nối giữa các id, tất cả các node đều "hướng tới" (kết nối tới) node cao nhất aka root node.

id[0] = 1 // node 0 kết nối tới node 1
id[1] = 2 // node 1 kết nối tới node 2
id[2] = 0 // node 2 kết nối tới node 0
id[3] = 3 // node 3 kết nối tới chính nó (root node)
Union find data structure
Union find data structure (Source: Princeton University - Coursera - Algorithms, Part I)
class UnionFind {
private:
    vector<int> ids;
public:
    UnionFind(int n) {
        for (int i = 0; i < n; i++) {
            ids[i] = i;
        }
    }

    ...
};

UF xây dựng kết nối giữa 2 node xoay quanh 2 method chính:

find(x)

Ta đã biết node x kết nối với node y đc biểu diễn là

ids[x] = y

Nếu node y chưa thực hiện kết nối tới node nào khác, vậy thì ta sẽ biết node y là root node.

ids[y] = y

Như vậy, ta cũng biết được root node của node x là node y.

Còn nếu như node y thực hiện kết nối tới node z (z là root node)?

ids[y] = z

Root node của node x sẽ là node z chứ ko phải node y, node y ko còn là 1 root node nữa.

Dựa theo quy tắc này, ở trong find() method, ta sẽ cần tạo vòng lặp để di chuyển từ input node tới root node của nó.

ids[x] = y
ids[y] = z
ids[z] = z

Start checking at node x, we get node y => check node y, we get node z => check node z, we get root node
int find(int x) {
    int runner = x;
    while(ids[runner] != runner) {
        runner = ids[runner];
    }
    return runner;
}

Sơ bộ thì find(x) sẽ tốn O(N) time complexity với N là số node mà con UF có (trong trường hợp toàn bộ node kết nối với nhau).

union(x, y)

Dựa vào việc xác định đc root node của mỗi node, ta có thể thực hiện việc kết nối 2 node với nhau.

Đầu tiên ta cần check 2 node này kết nối với nhau chưa đã? Chỉ cần 2 node này chung 1 root node là chứng minh đc chúng kết nối với nhau rồi.

Sau đó ta có thể connect 2 node bằng cách cho ids = y hoặc ids = x. Nhưng theo convention node x unions node y thì ids = y sẽ ok hơn.

void union(int x, int y) {
    int rootX = find(x);
    int rootY = find(y);
    if (rootX == rootY) return;
    ids[x] = y;
}

Vậy là union(x,y) cũng sẽ tốn tới O(N) time complexity cho 2 lần find()

Optimization

Sơ bộ như trên là ổn chạy được, nhưng tốc độ lại chậm, ta hoàn toàn có cách để cải thiện lên rất nhiều lần. Chỉ 1 method union(x,y) cũng tốn O(N), tưởng tượng ta thực hiện lặp lại union hàng ngàn (M) node đã được kết nối, thời gian lên tới O(N*M) thì sú.

Weighting improvement

Với việc kết nối các node tạo thành 1 graph dạng cây, ở cách sơ bộ, ta cứ cho 2 node kết nối thẳng zô, node này nối node kia, thì cuối cùng ta sẽ có 1 cái cây có chiều cao rất lớn. Điều này vô hình chung tăng thời gian cho find() lên trường hợp lâu nhất khi phải chạy qua cả cái cây để lên root node.

Ta có thể cải thiện điều này bằng cách keep track độ lớn (số node mà tree có) của cái tree đang chứa mỗi node. Khi kết nối 2 node, ta sẽ so sánh độ lớn 2 cái tree: root node của tree nhỏ hơn sẽ thực hiện kết nối root node của tree lớn hơn. Nhờ đó, độ cao của tree sau cùng sẽ chỉ cộng thêm rất ít hoặc gần như ko cộng tý nào.

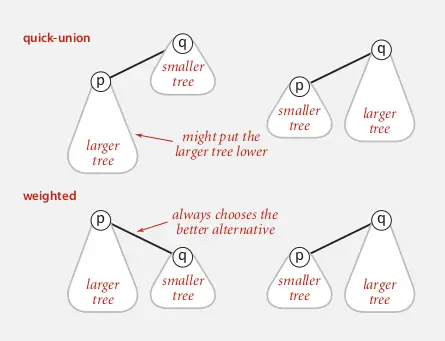
Union find weighting improvement
Union find weighting improvement (Source: Princeton University - Coursera - Algorithms, Part I)

Ta sẽ cần 1 array mới weights để lưu dữ liệu về độ lớn. Mỗi index trong weights sẽ được khởi tạo với giá trị 1

vector<int> weights;
...
UnionFind(int n) {
    for (int i = 0; i < n; i ++) {
        ...
        weights[i] = 1;
    }
}

Logic trong union(x, y) sẽ đc áp weights

void union(int x, int y) {
    int rootX = find(x);
    int rootY = find(y);
    if (rootX == rootY) return;
    if (weights[rootX] < weights[rootY]) {
        ids[rootX] = rootY;
        weights[rootY] += weights[rootX];
    } else {
        ids[rootY] = rootX;
        weights[rootX] += weights[rootY];
    }
}

Nhờ việc giảm độ cao của tree, find() và union(x, y) giờ đc tối ưu xuống còn O(logN).

Path compression improvement

Trong thg find(x), ta có thể nhận thấy mỗi lần ta muốn tìm root node cho 1 node, ta đều phải lội từ input node tời root. Nghe hơi oải... Mặt khác, ta lại nhận ra trong mọi node cùng connect với nhau, chúng đều có chung 1 root node, và method union() của ta giờ chỉ phụ thuộc vào root node là chính, vậy việc gì ta phải quan tâm tới mấy node khác nhỉ?

Ta có thể chỉnh sửa nho nhỏ trong find(x): Khi ta tiến đc tới root node, ta gán con root node này thẳng vô ids[input node] của ta luôn. Ưhy not??? Lmao. Nó đều ko gây ảnh hưởng gì tới node khác, vẫn đảm bảo kết nối với nhau thông qua root node. Với chỉnh sửa này, ta có thể chắc chắn rằng trong những lần find lặp lại sau, ta sẽ chỉ tốn có O(1) time.

Cuối cùng, tổng thể của Union Find sẽ là như sau:

#include <vector>

using namespace std;

class UnionFind {
private:
  vector<int> ids;
  vector<int> weights;

public:
  UnionFind(int n) {
    for (int i = 0; i < n; i++) {
      ids[i] = i;
      weights[i] = 1;
    }
  }

  int find(int x) {
    int runner = x;
    while (runner != ids[runner]) {
      runner = ids[runner];
    }
    ids[x] = runner;
    return runner;
  }

  void connect(int x, int y) {
    int rootX = find(x);
    int rootY = find(y);
    if (rootX == rootY) return;
    if (weights[rootX] < weights[rootY]) {
      ids[rootX] = rootY;
      weights[rootY] += weights[rootX];
    } else {
      ids[rootY] = rootX;
      weights[rootX] += weights[rootY];
    }
  }

  bool isConnected(int x, int y) {
    return find(x) == find(y);
  }
};

Sample questions